Valeurs financières d'un projet

Commençons par la théorie

Valeur Actuelle

Intéressons nous d’abord au paramètre Valeur Actuelle VA. La formule de calcul de la valeur actuelle d’un Flux de Trésorerie futur FT, étant donné un taux d’actualisation r, est:

Cette formule peut s’écrire de façon un peu plus explicite:

Cette expression montre que la Valeur Actuelle correspond au montant à placer aujourd’hui pour obtenir FT en fin de période si le taux d’intérêt par période est r.

En anglais, la formule devient:

avec

• PV = Present Value,
• CF = Cash Flow,
• r = Discount Factor

Facteur d’Actualisation

La formule de la Valeur Actuelle peut également être exprimée sous la forme:

CA est appelé Coefficient d’Actualisation.

En anglais la formule devient:

avec

• PV = Present Value,
• DF = Discount Factor, que l’on peut également noter Actual Rate, AR

Valeur Actuelle Net

La valeur actuelle nette, VAN , est une mesure de la rentabilité d’un investissement, calculée comme la somme des flux de trésorerie engendrés par cette opération, chacun étant actualisé de façon à réduire son importance dans cette somme à mesure de son éloignement dans le temps.

Exprimé autrement: Une valeur actuelle est la somme des flux de trésorerie, actuelles et futures, négatives ou positives. La valeur de chacun de ces flux doit être ajustée au risque et à la valeur de l’argent dans le temps.

La formule générique est la suivante:

Calcul de la VAN en utilisant la définition de la Valeur Actuelle décrite dans le paragraphe précédent, nous obtenons:

avec

• t désigne la période en cours, t=0 étant le moment de la prise de décision,
• T désigne la dernière période, dite horizon,
• VA, Valeur Actuelle,
• CA, Coefficient d’Actualisation,
• FT, Flux de Trésorerie

En anglais les formules deviennent donc:

avec

• NPV, Net Present Value,
• PV, Present Value,
• CF, Cache Flow,
• AR, Actual Rate

Il existe des variantes de cette formule, mais elles ne sont qu’une expression particulière de la formule générale précédente.

La première variante permet d’isoler l’investissement initial:

avec

• la valeur t varie de 1 à T, et non de 0 à T,
• I est l’investissement initial (I = FT0).

La seconde variante peut être intéressante, si l’on veut isoler/identifier certains frais, liés à la fin de vie du produit déployé:

avec

• la valeur t varie de 0 à T+1,
• FTT+1 représente des frais comme des coûts de démantèlement, par exemple.

Exemple 1: Appel d’offre concernant du matériel Nous avons deux fournisseurs finalistes, avec chacun une solution. Les comparaisons techniques sont terminées, la décision reste difficile à prendre. La comparaison financière n’est pas triviale, car en plus du coût d’achat, ont été négociés les frais de maintenance, et d’intervention sur site.

Paramètres	Fournisseur A	Fournisseur B
Coût d’achat	420 k$	445 k$
Maintenance matérielle	80 k$ (1)	30 k$ (1)
Maintenance logicielle	50 k$ (2)	15 k$ (2)
Service sur site	20 k$	20 k$

1. A partir de la 5ième année
2. A partir de la 3ième année.

Calculs « manuels »

Calculons les valeurs de VA pour chaque année, puis le cumul des VA pour obtenir la VAN, en utilisant directement des formules listées précédemment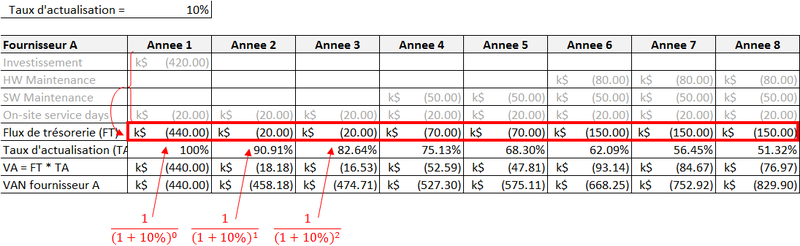

Même calcul pour le second fournisseur B:

Utilisation de Microsoft Excel

Des outils comme Excel fournissent des fonctions facilitant ces calculs.

Attention cependant aux conventions prises par Microsoft: la formule utilisée est la suivante:

Donc si vous voulez retrouver exactement les valeurs obtenues précédemment, il faudra effectuer les opérations suivantes (deux solutions possibles):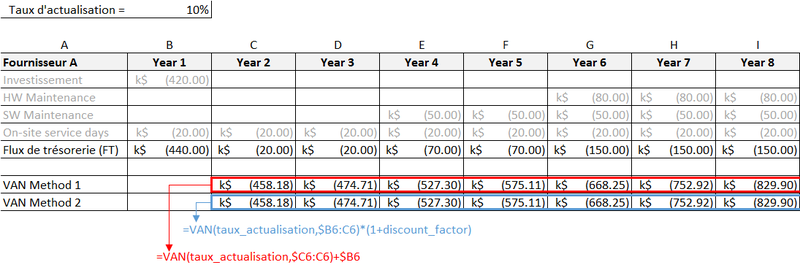

Conclusion de cet exemple

Maintenant que nous avons les deux tableaux, nous pouvons les comparer:

• Le fournisseur A est moins cher au départ, mais les coûts de maintenance sont relativement élevés,
• Le fournisseur B est plus cher, mais les frais de maintenance sont inférieurs,
• Sur la période étudiée, la solution proposée par le fournisseur B, est la plus intéressante (VAN égale à -660 k$ au lieu de -830 k$ pour le fournisseur A).

Importance de la période

Si nous entrons un peu plus dans le détail, la solution du fournisseur B est plus intéressante sur une certaine période de temps:

• En dessous de 4 ans, en effet, la VAN de la solution du fournisseur A (474 k$) est meilleure que celle du fournisseur B (499 k$),
• Ce n’est qu’au delà de 4 ans, que la solution du fournisseur B devient plus intéressante.

Quand il s’agit de matériel comme des serveurs, ou du stockage, nous pouvons nous poser la question de la pertinence de la période de calcul:

• La période d’amortissement de ce type de matériel est relativement courte (inférieure 6 ans),
• Les prix baissent en permanence (surtout pour le stockage): une baie de stockage de génération n+1, sera souvent moins chère à capacité égale, qu’une extension de la baie de génération n.

Il serait donc plus sensé de réduire la période de calcul. Si nous le faisons, en arrêtant la période de calcul à 3 ans, au lieu de 8 ans, le choix se porterait sur le fournisseur A, et non sur le fournisseur B comme dans notre première conclusion.

Nous voyons bien que

• Le calcul du paramètre VAN se fait toujours par rapport à une période spécifique. Si la période change, les conclusions peuvent également changer,
• Le choix de la période est donc cruciale,
• Et ce choix dépend du sujet traité, ou du cycle de vie des produits déployés.

Exemple 2: Business case d’un outil d’automatisation

Dans cet exemple, le projet consistait à améliorer la stabilitié, et la robustesse générale du réseau informatique de nos sites. L’idée globale était de mettre en place un outil permettant la vérification automatique de la configuration de chaque port, et de chaque composant réseau, par rapport à des règles prédéfinies par les administrateurs réseaux.

Contrairement au sujet précédent, nous sommes typiquement dans le calcul du Business Case d’un projet: les mesures à mettre en place font-elles réellement économiser de l’argent à l’entreprise ? Le coût investi dans la méthode choisie, compensera-t-il les gains financiers liés à une anomalie « réseau » d’un site (site de production) ?

Pour cela, nous avons comparé deux solutions

• Solution 1: On ne change rien, ou presque. On se contente de systématiser des vérifications manuelles,
• Solution 2: On déploie un logiciel capable d’effectuer ces vérifications automatiquement.

Informations communes aux deux hypothèses:

• Nous avons 10 sites de production,
• Le coût journalier de la main d’oeuvre: 100 k$ par an,
• Le coût des arrêts de production pour l’année en cours est de 400 k$

Les informations disponibles pour la solution 1 sont:

• Il a été estimé à 1/2 jour/homme, la charge nécessaire aux vérifications manuelles, la première année, puis 1/3 jours/homme, les années suivantes,
• Les opérations de vérifications manuelles permettraient de réduire le nombre d’arrêts de production d’environ 30% la première année, et 50% la seconde année, et 60% les années suivantes.

Les informations disponibles pour la solution 2 sont:

• Le coût de la solution logicielle est 270 k$, maintenance annuelle 48 k$,
• La plateforme matérielle à déployer coûte environ 25 k$ (maintenance annuelle 2.5 k$),
• L’installation du logiciel, ainsi que sa configuration coûtent 60 k$,
• Il faut compter le coût de l’administration du logiciel (un peu moins d’un jour par semaine).

Pour la solution 1, le tableau des valeurs VA, et VAN est le suivant: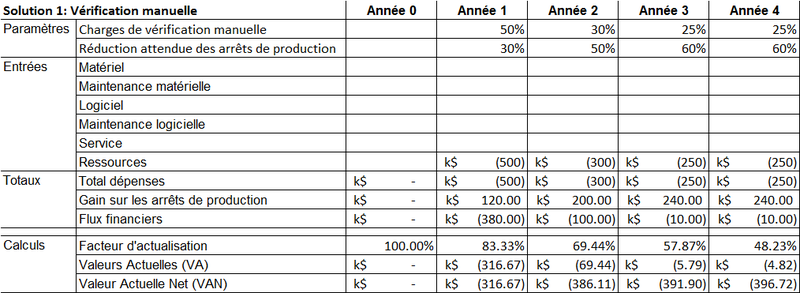

Pour la solution 2, nous avons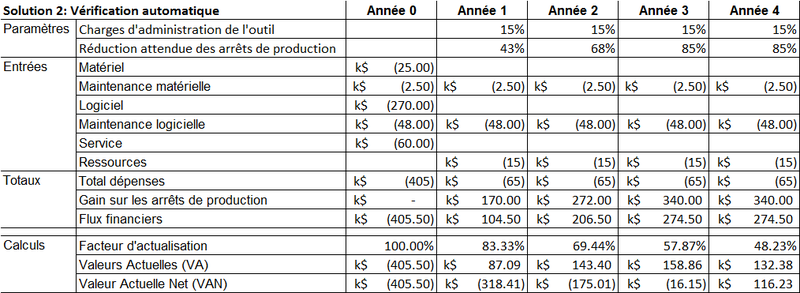

Conclusion de cet exemple

La meilleure solution est clairement la solution 2: dès la seconde année, la VAN de la solution 2 est supérieure à celle de la solution 1, et elle devient positive entre la 3ième et la 4ième année, alors que la solution 1 reste « déficitaire » sur toute la période.

On voit bien dans cet exemple, que toute la complexité du calcul de la VAN réside dans la collecte des valeurs d’entrée, et de leur estimation.

Pendant toute l’élaboration de l’étude, les discussions ont principalement porté sur les valeurs d’entrées:

• Comment estimer les coûts d’un arrêt de production?
• Comment évaluer le temps nécessaire à la vérification manuelle de tous les éléments réseau d’un site?
• Comment estimer le gain que ces vérifications peuvent apporter?

Nous reviendrons sur ce point dans le paragraphe suivant.

Les inconvénients de l’indicateur VAN

La VAN est un outil puissant, mais il ne constitue pas l’outil idéal, pour plusieurs raisons:

• d’abord, comme je l’ai déjà mentionné précédemment, la collecte des données d’entrée, et leur estimation financière est loin d’être triviale. Ces données d’entrée peuvent faire l’objet de discussion / contestation. Personnellement, je pense qu’il ne faut pas utiliser la VAN, si les données d’entrées sont trop complexes ou sujettes à trop de discussions,
• La VAN est très sensible au taux d’actualisation,
  • Choisir un taux d’actualisation élevé rendra le projet plus cher, donc plus difficilement justifiable,
  • Choisir un taux d’actualisation faible rendra le projet plus abordable / attractif, mais il sera également plus fragile aux écarts, vous disposerez de plus faibles marges.

Commentaires

Signification du taux d’actualisation

D’un point de vue gestion de projet, le taux d’actualisation peut-être considéré comme un paramètre de gestion de risque, ou une marge d’erreur. Ce qui compte en fait, c’est l’écart entre le taux d’actualisation, et le coût du capital pour l’entreprise (le taux d’inflation, ou les taux d’intérêt d’emrunt)

Choisir de faire le calcul avec un taux d’actualisation élevé

• augmente l’écart entre le coût de l’argent « réel » et le coût de l’argent choisi pour le projet,
• augmente le coût d’un projet,
• réduit la VAN initiale (donc peut remettre en cause votre Business case),
• mais si la VAN reste favorable au projet, cela veut dire que vous pourrez vous permettre quelques écarts, sans que cette VAN ne devienne négative.

Réciproquement, choisir un taux d’actualisation faible

• réduit le coût du projet,
• augmente la VAN initiale, et donc, favorise votre Business Case,
• mais le moindre écart financier, réduira la VAN à une valeur proche de 0 ou une valeur négative, avec le risque de perdre la justification du projet.

Concrètement, sur des sujets courts, avec peu de risques, il vaut mieux choisir un taux d’actualisation proche des valeurs utilisées par l’entreprise, surtout en cette période (faible inflation, et faibles taux d’intérêts).

Mais sur des sujets plus longs, ou plus risqués, il vaut mieux choisir un taux d’actualisation un peu plus élevé, pour vous prémunir contre des fluctuations, soient internes au projet (dérive budgétaire), soit externes (fluctuations monétaires euros-dollars défavorable par exemple).

L’importance des données d’entrées

Comme déjà évoqué dans l’exemple 2, la collecte des informations nécessaires au calcul de la VAN est donc le principal challenge. Il faut que ces informations soient exhaustives, précises, et argumentées.

• Exhaustives: pour que le calcul reflète au mieux la réalité du projet, ou de la solution à déployer, Précises: parce que, dans le cas de faibles différences, une erreur de quelques pourcents peut conduire à l’inversion des conclusions,
• Argumentées: parce que la solidité de votre Business Case (donc de votre projet), repose sur ces valeurs d’entrées

Ce dernier point me semble particulièrement important:

En début de projet:

Si l’un vos stakeholders (partie prenante), remet en cause vos conclusions, il le fera en contestant les données d’entrée, pas le calcul lui-même. Dans l’exemple 2, il serait très facile de « discuter » les pourcentages de réduction des coûts liés aux arrêts de production, ou la charges des administrateurs réseau pour effectuer la vérification manuelle. Ces deux valeurs n’ont pas été données au hasard, elles correspondent à des mesures et des statistiques basées sur la réalité.

En cours de projet

Comme je l’ai dit en introduction, Le Business Case est la raison d’être du projet. Avec la méthode Prince2, une évolution négative du Business Case peut conduire à l’arrêt d’un projet. Il faut donc être capable de ré-évaluer périodiquement la VAN, pendant l’exécution du projet, lorsque les conditions changent (par exemple le prix du logiciel est supérieur à l’estimation initiale). Si vous ne conservez pas une trace de vos calculs, et des données d’entrée, vous ne serez pas capable de réaliser ces mises à jour, ou vous perdrez beaucoup de temps à refaire les calculs initiaux pour les comprendre.

En fin de projet (pendant la clôture)

Il est également important de conserver l’historique des ré-évaluations, des argumentations, et des décisions de continuer le projet (ou pas). Toutes ces informations constituent la « traçabilité » du projet.

Autres indicateurs

L’indicateur VAN peut-être compléter par d’autres indicateurs.

Le Taux de rentabilité interne (TRI)

Le Taux de Rentabilité Interne (TRI, en anglais : IRR, Internal Rate of Return) est un taux d’actualisation qui annule la valeur actuelle nette d’une série de flux financiers. Le TRI est la résolution de l’équation suivante:

Si la formule semble très proche de celle de la VAN, l’approche est cependant différente:

• Avec la VAN, le taux d’actualisation fait partie des données d’entrée,
• Avec le TRI, le taux d’actualisation n’est plus une hypothèse, mais une valeur calculée.

Si le TRI est supérieur au taux d’actualisation du capital (Coût moyen pondéré du capital, CMPC, en anglais Weighted Average Cost of Capital, WACC) d’une entreprise, alors la Valeur Actuelle Net du projet est positive (le projet est « rentable »).

La résolution de cette équation est relativement complexe à la main (équation de degré T à une inconnue):

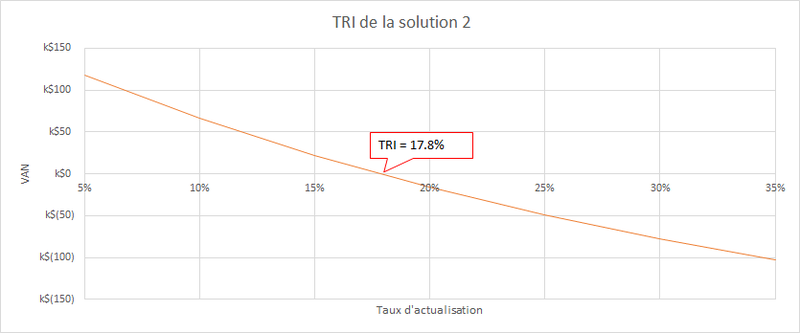
Heureusement, nous avons des outils pour le faire à notre place, ce que nous allons voir en appliquant le calcul à l’exemple 2.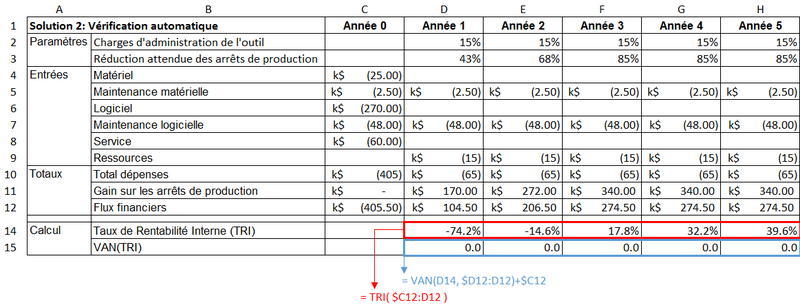

Délai de récupération du capital investi

Cet indicateur, en anglais Payback Period, correspond au nombre d’années (ou de mois) nécessaires pour que le cumul des flux de trésorerie atteignent le capital investi.

avec

• I, capital investi
• n, le délai de récupération,
• FT_t Flux de trésorerie.

Conclusion

Une justification claire, et argumentée, est un des facteurs de réussite d’un projet, car elle constitue un très bon rempart contre les remises en cause, et même les changements demandés en cours d’exécution.

Au delà des arguments techniques, les indicateurs financiers comme ceux dont nous venons de parler, sont d’excellents outils, parce que

• Ils sont factuels,
• Ils peuvent être plus explicites que les arguments qualitatifs.

Les indicateurs financiers constituent également un vocabulaire commun entre le groupe projet, et le client, qui travaillent souvent dans des domaines complètement différents (informatique, et production, par exemple).